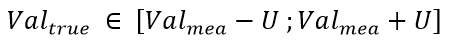
Uncertainty in measurement and declaration of conformity

Many norms tend to provide solutions to this problem. Among these is ISO 14253-1 :2013 norm, (Geometrical product specification (GPS) – Inspection by measurement of workpieces and measuring equipment), as it establishes specific areas such as these below :

The specification area corresponds to the area within which the true value shall be found, so that the measured object can perform its required function. The non-conformity areas are thus rejection areas. If a measurement is in the conformity area, we thus guarantee that the true value of the object is compliant. The uncertainty areas are areas within which we cannot declare on conformity. Then, in accordance with the directives of the norm, we have to find a
more efficient measuring process, enabling us to have less uncertainty and avoid any doubt. This uncertainty area cannot be obviously reduced to zero and it will be up to the contractual partners to make an agreement to decide on this matter.

In practice, manufacturers do not explicitly take the uncertainty in measurement into account. So, if an objet is outside the conformity area, while being very close, the latter shall ask his/her customer for a derogation in order to know if they accept or reject the object that has become an issue. This common practice comes from the fact that there is always a gap between the demand and the real need of the customer. So, if the manufacturers become aware of the uncertainties in measurement (in order to come close to the real need), and seeks to reduce them, then the conformity area will be increased.

A link exists between uncertainty in measurement and tolerance to check : the capability. The latter applies less to the instrument than to the process ; in this case, we speak of capability of the measuring processes.

The concept of normalised « capability of the measuring processes »: the NF ISO 22514-7 (2013) norm

It is here one finds the ISO22514-7 :2013 norm (Statistical methods in process management – Aptitude and performance) which defines the ratio of performance as well as the aptitude indicator.
The performance ratio, as well as the aptitude indicator, can be defined at the level of the system or the measuring process. The performance ratio is defined by the following equation : Q=2.U/T in which U is the expanded uncertainty, and T the tolerance (the norm recommends, for the measuring process, Q<30%, and Q<15% for the measuring system). Likewise, an aptitude indicator is defined by : C=0,3.T/(h.u) in which T is the tolerance, u the standard uncertainty and h a coefficient (equal to 3 for the measuring process and to 6 for the measuring system), the norm recommends C>1,33 in both cases.
It is important that we should note that C & Q coefficients take values defined by the customer and the supplier. There is no absolute rule, that is the reason why the norm only makes recommendations and does not impose values.

By taking C coefficient into account, one can notice that, the bigger the coefficient, the smaller the uncertainty against the tolerance (a more expensive method) and vice versa. The optimal coefficient is thus the best compromise between supplier and customer.

In both cases, there remains a grey area for objects that would be found in the uncertainty zone.

NF ISO/CEI Guide 98-4 (2013) norm benefits

ISO Guide 98-4 :2013 norm (The role of uncertainty in measuring in the declaration of conformity) is in fact a transposition - on the international plane - of the 2008 corrected version of 1995 JCGM 100 GUM Document: Guide for the expression of uncertainty in measuring).

This norm is based on the notions of “customer's risk“ and “supplier's risk“ in order to define strategies that allow, for example, a guaranteed constant customer's risk. (This approach is particularly useful for defining the risk, for the objects located in this grey area, to be deemed compliant).

By definition, a customer's risk is the probability, of the customer receiving a non-compliant object, where it has been deemed compliant. This notion has often been interpreted as the probability that a true value may be outside the specification area. This interpretation is not totally true, because, before such a problem arises, the object must be first manufactured. Customer's risk appears at two stages, when the product is made, and when the measuring is
carried out at the time of the control.

The norm defines two customer's risks, global risk and specific risk.

• Global risk stands for the product of the probability of producing a non-compliant product multiplied by the probability of measuring and finding the product compliant.
• Specific risk stands for the probability that the measured object can be outside a predetermined tolerance.

As far as supplier's risk is concerned, the norm defines this risk as the probability of defining a compliant object as non-compliant. These two aspects remain similar to those previously addressed (and they are calculated in more or less the same way).

Outlook

This norm leads us to see metrology from a new angle. The very fact of checking the measuring instruments being unsufficient, so it is also telling to focus on the process related to the measured object, in so far as what is at stake here is ensuring the ability to check the tolerance relating to the object (the capability of the measuring processes). An in-depth study of these different aspects leads to a study of customer/supplier risk, and thus finding out how
to cut the induced costs, and so, lessening the tolerance in order to end up finding a consensus between customer and supplier. The day by day challenge is that, by reducing the uncertainty in measuring, the conformity area can be increased, and thus in turn increasing productivity by enlarging its conformity area.